개발해요

https://www.acmicpc.net/problem/2186

안녕하세요, 이륙사입니다.

풀이

위 문제는 DFS를 사용하는 그래프 탐색 문제였습니다. 하지만 골드3에 정답률이 20퍼센트대인 것을 보아, 기본적인 DFS 문제와는 조금 다르다는 것을 짐작할 수 있는데요.

움직일 수 있는 경우의 수

먼저, 특정 위치에서 상하좌우로 한 칸씩 이동하는 것이 아니라 k칸씩 이동이 가능합니다. 즉, 아래 그림의 X표시된 곳으로 한번에 점프해서 이동할 수 있습니다. 따라서 k <= 5이므로, 매 위치마다 4 * 5 = 최대 20가지의 움직임이 가능합니다.

중복 방문

또 특이한 점은 갔던 곳을 다시 갈 수 있다는 것입니다. 중복해서 방문할 수 있기 때문에 현재 조건만 봐선 DFS가 아니라 매 위치마다 방문 가능한 모든 곳을 탐색하는 brute force 문제로 보는게 더 정확할 것 같습니다.

그럼 전부 확인하면서 풀 수 있을지 알아보기 위해 시간 복잡도를 계산해보겠습니다.

• 최대 노드 개수 = N * M = 10,000개,
• 매 위치마다 방문을 고려할 가지수 = 20개
• 단어 길이 <= 80

최대 80번을 움직이는데 한 번 움직일 때마다 20곳을 고려해야 하므로, 10,000 * 20 ^ 80 = 100자리가 넘는 수가 나옵니다. 따라서, 전부 확인하는 방식으로는 시간안에 해결할 수가 없습니다. 그러면 어떻게 시간을 단축시킬 수 있을까요?

📌3차원 그래프

2차원 그래프가 주어졌지만, 사실은 3차원 그래프로 생각할 수 있습니다. 같은 위치를 방문하더라도 영단어의 몇 번째 인덱스에 쓰였느냐에 따라 다른 노드로 볼 수 있기 때문입니다.

예) 단어: "ABAB", K = 2

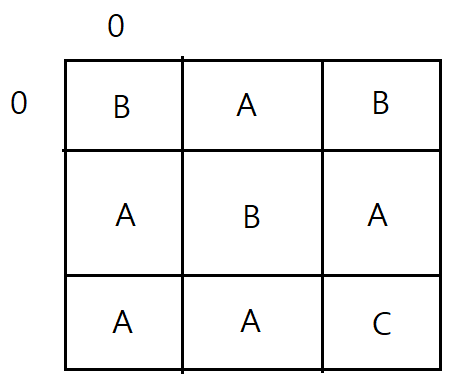
ABAB를 찾고 있고, (0, 1)에서 탐색을 시작하는 상황을 가정해보겠습니다. 그러면 B인 (0, 0), (0, 2), (1, 1)로 갈 수 있는데, (0, 0)으로 가보겠습니다. K=2이므로, (0, 1), (1, 0), (2, 0)으로 갈 수 있습니다. 그리고 문제의 중복 상황인 (0, 1)로 다시 가보겠습니다. (0, 1) -> (0, 0) -> (0, 1)이 됐습니다. 여기서 3개의 B로 갈 수 있으므로 3개의 ABAB 경로를 찾을 수 있습니다. 즉, (0, 1)을 ABAB의 3번째 순서(인덱스 2)로 방문하면 언제나 3개의 경로를 찾을 수 있다는 뜻입니다. 이것을 기록해놓으면 (1, 2) -> (0, 2) -> (0, 1)의 경로로 탐색을 할 경우 3개의 B에 다시 방문하지 않더라도 3개의 경로가 있다는 것을 바로 알 수 있습니다. => 메모이제이션

경로를 못찾았던 위치도 마찬가지로 0을 기록해서 해당 위치를 특정 순서로 방문하면 더이상 탐색하지 않을 수 있습니다.

쉽게 말하면 같은 (0, 1)의 A를 방문하더라도 이것을 ABAB[0]으로 사용했는지 ABAB[2]로 사용했는지에 따라 다른 노드가 되는 것입니다. 우리가 같은 방안에 있더라도 그 날짜가 오늘이었는지 어제였는지에 따라 다른 상태라고 생각하면 이해하기 편할 것 같네요. 

따라서 이 문제는 [행][열][인덱스]로 구성된 3차원 그래프 DFS + 다이나믹프로그래밍 혹은 DFS + 메모이제이션 문제였습니다. 

※ BFS를 사용하면 큐에 너무 많은 데이터가 들어가서 메모리 초과가 난다고 하네요!

※ 각 위치를 노드로 표현해보면 Node(문자, 행, 열, 인덱스)로 할 수 있습니다.

생각 과정

1. 영단어 경로를 찾기 조건을 만족하는 노드들을 방문하는 그래프 탐색문제라는 것을 확인한다.
2. 특정 위치에서 이동 가능한 경우의 수와 중복 방문이 가능하다는 것을 확인하고, 완전 탐색으로 풀었을 때의 시간 복잡도를 계산해본다.
3. 시간 복잡도가 정말 크다. 복잡도를 줄이기 위한 추가 고려 사항을 생각해본다.
4. 특정 노드를 방문하더라도 단어의 몇 번째 문자를 확인하느냐에 따라 node state가 다르다는 것을 이해한다.
5. 따라서 index까지 고려하는 3차원 그래프 탐색문제이다. 중복 방문 처리가 가능하기 때문에 시간을 단축시킬 수 있다.

코드

import java.io.BufferedReader
import java.io.InputStreamReader
import java.util.*

var answer = 0
var rowSize = 0
var colSize = 0
lateinit var target: CharArray // 찾으려는 영단어 문자 배열
lateinit var board: Array<CharArray> // 2차원 그래프
val dNext = mutableListOf<Pair<Int, Int>>()
lateinit var visited: Array<Array<IntArray>> // 3차원 그래프 -> [row][col][몇번째에 도착했는지]

fun main() = with(BufferedReader(InputStreamReader(System.`in`))) {
    val st = StringTokenizer(readLine())
    rowSize = st.nextToken().toInt()
    colSize = st.nextToken().toInt()
    val moveLimit = st.nextToken().toInt()
    board = Array<CharArray>(rowSize) {
        readLine().toCharArray()
    }
    target = readLine().toCharArray()
    
    // -1: 첫 방문, 0: 방문했었지만 경로가 없었다, 1 이상: 발견한 경로 수
    visited = Array(rowSize) {
        Array(colSize) {
            IntArray(target.size) { -1 } 
        }
    }

    // 상하좌우 K칸 이동 경우의 수
    for (i in 1..moveLimit) {
        val up = Pair(-i, 0); val down = Pair(i, 0)
        val left = Pair(0, -i); val right = Pair(0, i)
        dNext.addAll(listOf(up, down, left, right))
    }

    // 모든점을 시작점으로 탐색
    for (i in 0 until rowSize) {
        for (j in 0 until colSize) {
            if (board[i][j] == target[0]) {
                answer += findRouteCount(i, j, 0)
            }
        }
    }

    print(answer)
}

fun findRouteCount(row: Int, col: Int, index: Int): Int {
    if (index == target.size - 1) { // 단어를 찾았다
        return 1
    }

    var count = 0 // 지금 위치에서 찾을 수 있는 경로 수를 저장할 변수

    for (i in dNext.indices) {
        val nextRow = row + dNext[i].first
        val nextCol = col + dNext[i].second

        if (nextRow !in 0 until rowSize || nextCol !in 0 until colSize) continue
        if (board[nextRow][nextCol] != target[index + 1]) continue // 그래프 범위 밖
 
        // 이전에 방문한 곳일 경우
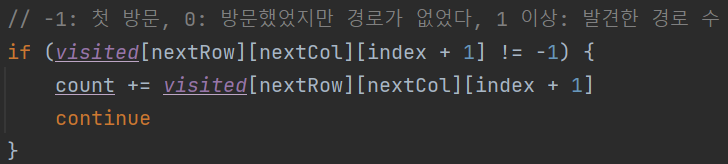
        if (visited[nextRow][nextCol][index + 1] != -1) {
            count += visited[nextRow][nextCol][index + 1]
            continue
        }

        count += findRouteCount(nextRow, nextCol, index + 1)
    }

    // 경로를 찾지 못했으면 0, 찾았으면 0보다 큰 수가 저장된다
    visited[row][col][index] = count
    return count
}

https://www.acmicpc.net/problem/13164

안녕하세요, 이륙사입니다.

풀이

위 문제는 비용이 키 차이와 관련있다는 사실에서부터 시작하는 문제였습니다.

인접한 원생들의 키 차이를 값으로 갖는 새로운 수열을 구합니다. 그리고 그 수열의 합에서 값이 가장 큰 k-1개의 값을 빼면 그것이 정답이 됩니다. 왜냐하면 (큰 키 - 작은 키)의 값은 그 사이에 있는 원생들간 키 차이의 합과 같기 때문입니다. 그리고 아래 예시처럼 조를 k개로 나누면 k-1개의 경계가 생기며, 그 경계에 해당하는 차이 값들만 비용을 계산하는데 사용되지 않습니다. 따라서, 전체 차이의 합에서 가장 큰 k-1개를 빼주면 그것이 답이 됩니다.

예)

7, 3

1 3 5 6 10 16 19

또한, 전체 값의 합에서 가장 큰 값들을 빼주기 때문에 그리디 유형의 문제라고 할 수 있습니다. 

생각 과정

1. 학생 수가 최대 300,000이므로, 전부 확인해볼 순 없다.
2. 비용은 조에서 가장 키가 큰 학생과 가장 작은 학생의 차이다 --> 값의 차이에 주목한다.
3. 인접 원소들간 차이에 대해서도 생각해볼 수 있다.
4. 가장 키가 큰 학생과 작은 학생의 키 차이는 두 학생 사이에 있는 학생들간 키 차이의 합이란 것을 발견한다.
5. 조를 나누어본 결과, 비용의 합은 전체 키 차이의 합에서 가장 큰 k-1개의 값을 뺀 값이라는 것을 확인한다.

코드

import java.io.BufferedReader
import java.io.InputStreamReader
import java.util.*
import kotlin.math.sqrt

fun main() = with(BufferedReader(InputStreamReader(System.`in`))) {
    val (n, k) = readLine().split(" ").map{ it.toInt() }
    val st = StringTokenizer(readLine())
    val gaps = IntArray(n) { st.nextToken().toInt() }
    
    // 인접 학생간 키차이를 값으로 갖는 수열
    for (i in 0 until n-1) {
        gaps[i] = gaps[i+1] - gaps[i]
    }

    // k개로 나누면 k-1개의 경계가 생긴다
    gaps.sort() // 전체에서 값이 큰 경계 k-1개를 빼기 위해 먼저 정렬한다  
    
    // 가장 큰 k-1개를 뺀 나머지를 모두 더한다
    val min = (0 until (n-1)-(k-1)).sumOf { i -> gaps[i] }
    print(min)
}

https://www.acmicpc.net/problem/22862

풀이

1. 투포인터 방법(left, right)을 사용한다.
2. 짝수, 홀수 카운팅(evenCount, oddCount)를 위한 변수와 최소 길이를 저장할 정답(answer) 변수를 선언한다. right 포인터는 0부터 시작한다.
3. right 포인터로 홀수를 k+1개 찾을 때까지 숫자를 차례대로 확인하면서 홀, 짝의 개수를 카운팅한다.
4. 홀수가 k+1개가 됐을 때,
   1. 지금의 짝수 개수가 k+1번째 홀수의 왼쪽에 있는 홀수 k개를 지웠을 때의 연속 짝수 길이가 된다. 따라서 이것을 지금까지 구한 정답과 비교한다
   2. left를 현재 구간의 첫번째 홀수 인덱스 + 1이 될 때까지 증가시킨다. 그 과정에서 짝,홀수의 개수를 감소시킨다.
5. 3, 4번 로직을 right가 전체 수의 길이보다 크거나 같아질 때까지 반복한다.
6. 홀수가 k개 이하일 경우를 대비하기 위해, 3,4,5번 반복문 종료 후 eventCount + oodCount == 전체 수의 길이인지 확인한다. true이면 eventCount가 정답이 된다. 

생각 과정과 후기

실버1이었는데 개인적으로 정말 정말 어려웠다.

우선 홀수를 어떻게 지워야 가장 긴 짝수를 만들 수 있을지 고민했다. 그리고 인접한 홀수들을 지울 때 가장 긴 짝수를 구할 수 있을 거라고 생각했다. 왜냐면, 만약 아래처럼 띄엄띄엄 지운 케이스가 정답이라고 가정해보면, 왼쪽에 있는 더 긴 범위가 정답일 것이다. 하지만 오른쪽 범위에서 지운 홀수 대신 가운데에 있는 홀수를 지우면 구간을 만들 수 있기 때문에 가정에 모순이 된다. 그래서 띄엄띄엄 지웠을 때는 정답을 구할 수 없다고 논리적으로도 확신할 수 있었다.

이제 구현만 하면 되는데, 그게 쉽지 않았다.

처음에는 홀수들의 인덱스를 리스트에 따로 저장해서 차례대로 k개를 지울 때마다 연속 짝수의 길이를 구하려고 했다. 하지만 지울 때마다 양 끝에 있는 홀수들의 바깥쪽에 짝수가 있는지, 있다면 몇개나 있는지를 알아내는 것이 쉽지 않았다. 그래도 나름대로 코드를 짜서 돌려봤는데 잘 안됐고, 결국 다른 분들 풀이를 참고했다.

풀이법을 어떻게 떠올릴 수 있었을까?

1. 인접한 홀수들을 왼쪽에서 오른쪽 순서대로 탐색한다 --> 구간을 옮긴다는 개념을 떠올릴 수 있다.

2. 홀수 범위를 알더라도 양 옆에 짝수가 어떻게, 몇 개나 있는지도 알아야 한다 -> 짝, 홀을 모두 고려해야 한다.

==> 순서대로 모든 수를 탐색하면서 + 짝 홀 두 가지를 다 신경써야 한다 + 구간을 옮긴다 -> 투포인터

이런 과정으로 떠올릴 수 있지 않았을까?

코드

import java.io.BufferedReader
import java.io.InputStreamReader
import java.util.*
import kotlin.math.max

fun main() = with(BufferedReader(InputStreamReader(System.`in`))) {
    val st = StringTokenizer(readLine())
    val numberSize = st.nextToken().toInt()
    val removeSize = st.nextToken().toInt()
    val numbers = with(StringTokenizer(readLine())) {
        IntArray(numberSize) {
            this.nextToken().toInt()
        }
    }

    var answer = 0
    var left = 0
    var right = 0
    var evenCount = 0
    var oddCount = 0

    while (right < numberSize) {
        if (numbers[right++] % 2 == 0) evenCount++
        else oddCount++

        // k+1번째까지 찾아야 k번째 홀수 오른쪽에 있는 짝수들을 계산할 수 있다.
        if (oddCount > removeSize) {
            answer = max(answer, evenCount)

            // 가장 왼쪽에 있는 홀수를 찾을 때까지 증가시킨다
            while (numbers[left] % 2 == 0){
                left++
                evenCount--
            }
            left++ // 투포인터 범위를 가장 왼쪽에 있던 홀수 오른쪽부터 시작하도록 옮긴다
            oddCount--
        }
    }

    if (evenCount + oddCount == numberSize) {
        answer = evenCount
    }
    print(answer)
}

https://www.acmicpc.net/problem/1697

풀이

DP로 풀 수 있을 것 같았는데 방법이 떠오르지 않아서 우선 BFS를 사용했다. 매초마다 이전 위치들에서 도착할 수 있는 모든 위치로 움직이기 때문에 가장 처음 목표지점에 도착했을 때가 최단 시간이 된다.

또한, 곱하기2로 범위를 절반씩 줄일 수 있으므로 O(log^N) 시간으로 문제를 해결할 수 있다

BFS 과정에서 당연하지만 이전에 방문했던 점은 다시 방문하지 않아야 하는데, 이전보다 시간이 더 흐른 상태에서 같은 연산을 반복하기 때문이다. 따라서 방문표시를 할 배열이 필요한데, 크기를 어느 정도로 잡아야할지 고민이 됐다. 예를 들어 50,001 (x2) -> 100,002 (-1) (-1) -> 100,000 와 같이 최대 범위를 초과했다가 마이너스로 가는 경우도 있을 것 같았기 때문이다. 

결과적으로, 50,001 (-1) -> 50,000 (x2) -> 100,000처럼 최대 범위를 넘어서는 경우보단 숫자를 먼저 몇 번 빼고 x2를 하는게 항상 더 빨리 갈 수 있다. 그리고 절반인 50,000을 기준으로 숫자가 커질수록 그 차이는 훨씬 커진다.

ex)

1. 50,004 (x2) -> 100,008 (-8) -> 100,000 ==> 9번

2. 50,004 (-4) ->  50,000 (x2) -> 100,000 ==> 6번

따라서, 방문 가능 범위를 0 ~ 100,000으로 제한해도 문제를 해결할 수 있다.

개인적으로 처음엔 여기까지 생각하지 못해서 안전하게 최대 200,000까지 방문 가능하도록 했는데, 정답을 받을 수 있었다.

이후에 궁금해서 찾아봤는데, 최대 범위를 넘어서는 경우가 없는건 k의 최대 값이 짝수이기 때문이었다.

9 -> 15  ==>  9 -> 8 ->16 -> 15 의 케이스처럼, 최대 값이 홀수라면 최대 값을 넘어서고 마이너스로 가는 케이스가 존재할 수 있기 때문이다.

하지만 처음 문제를 풀 땐 생각하기 어려울 수 있기 때문에, 그럴 땐 범위를 충분히 안전하게 설정해서 푸는 게 좋을 것 같다.     

코드

import java.io.*
import java.util.*

// 250_000을 이상인 모든 수 n은
// (n * 2) 이후 -1씩 계산해주는 것보다
// -1을 먼저 몇 번 빼고 n * 2를 하는 게 항상 더 빠르다
// ex) 250_001 * 2 = 500_002 -> 500_000 ==> 3번 계산
// ex) 250_001 -> 250_000 -> 500_000 ==> 2번 계산
// 250_001에서 수가 커질 수록 차이는 더 커진다.
const val MAX_POSITION = 100_000

fun main() = with(BufferedReader(InputStreamReader(System.`in`))) {
    val input = readLine().split(" ")
    val myPosition = input[0].toInt()
    val goal = input[1].toInt()

    val visited = BooleanArray(MAX_POSITION + 1)    // 방문 처리 배열
    val queue: Queue<Pair<Int, Int>> = LinkedList() // 위치, 지난 시간
    queue.offer(Pair(myPosition, 0))
    visited[myPosition] = true

    while (queue.isNotEmpty()) {
        val pair = queue.poll()
        val position = pair.first
        val time = pair.second

        if (position == goal) { // 동생을 찾았으면 종료
            print(time)
            return
        }

        // -1을 거쳐가는 최단경로는 존재할 수 없다
        val nextPosition1 = position - 1
        if (nextPosition1 >= 0 && visited[nextPosition1].not()) {
            visited[nextPosition1] = true
            queue.offer(Pair(nextPosition1, time + 1))
        }

        // 현재 위치가 동생의 위치보다 크면 증가 연산을 할 필요가 없다.
        if (position < goal) {
            val nextPosition2 = position + 1
            // 최대 범위를 넘었다가 왼쪽으로 가는 경로보다 더 빠른 경로가 항상 존재한다.
            if (nextPosition2 <= MAX_POSITION && visited[nextPosition2].not()) {
                visited[nextPosition2] = true
                queue.offer(Pair(nextPosition2, time + 1))
            }

            val nextPosition3 = position * 2
            if (nextPosition3 <= MAX_POSITION && visited[nextPosition3].not()) {
                visited[nextPosition3] = true
                queue.offer(Pair(nextPosition3, time + 1))
            }
        }
    }
}