https://programmers.co.kr/learn/courses/30/lessons/49191
코딩테스트 연습 - 순위
5 [[4, 3], [4, 2], [3, 2], [1, 2], [2, 5]] 2
programmers.co.kr
안녕하세요, 이륙사입니다.
오늘 프로그래머스에서 순위라는 문제를 풀어봤는데 어렵다는 생각이 들었습니다. 그래서 제 힘으로 풀진 못하고 다른 분들 풀이를 찾아봤는데, 대부분 플로이드 와샬을 사용해서 푸셨더라구요. 그런데 왜 꼭 그래야 하는지가 명쾌하게 나와있지 않아서 좀 답답했습니다. 그러던 중 DFS만을 사용해서 푸신 분이 계셔서 해당 풀이를 공부하고 공유해보려고 합니다.
정리
- 문제를 그래프로 표현할 수 있다: 선수(노드), 경기(엣지) 승패(엣지 방향)
- 이길 수 있는 선수 + 지는 선수의 합이 n-1인 선수는 순위가 확정된 것이다.
- 각 선수마다 누구에게 이기고 지는지를 모두 확인한다. 즉, (a > b), (b > c) -> (a > c) 처럼 건너 관계까지 모두 확인한다. --> DFS를 사용한다
- a > b를 확인할 때, 반대로 b < a 라는 정보도 확인할 수 있다. 즉, 각 선수마다 이기는 정보에 대한 DFS 탐색을 진행하면 지는 관계까지 모두 확인할 수 있다. --> 그러므로 각 선수를 시작노드로 각각 DFS를 진행한다
풀이
두 선수가 이기고 지는 관계를 그래프의 노드, 엣지, 엣지방향으로 나타낼 수 있습니다.
엣지 방향을 어떻게 하든 상관 없지만 저는 노드에서 나가는 방향이 이기는 것, 들어오는 방향이 지는 것으로 표현했습니다. 대회에서 이기면 경기를 더 치룰 수 있지만 지면 짐싸서 집으로 돌아와야 하기 때문이죠. 물론 문제에선 그렇지 않지만요!ㅋㅋ
그래프
근데 왜 그래프로 생각해야 할까요? '그냥 그렇게 하는게 자연스러우니까, 당연하니까, 문제 분류가 그래프니까' 라고 생각할 수도 있지만, 나름의 이유를 부여할 수도 있습니다.
이를 단순 리스트로 표현하면 [1, 3], [3, 2]가 됩니다. 그리고 이 정보만으론 순위를 판별할 수 없습니다. 그냥 '1 > 3, 3 > 2 이니까 당연히 1 > 2고, 1 > 3 > 2가 되지'라고 생각할 수 있지만, 사실 이것이 그래프적으로 사고한 겁니다. (1 -> 3), (3 -> 2)의 과정을 거친것이죠. 단순 배열처럼 생각한다면 그 너머에 있는 관계까지 파악하는 것이 힘듭니다.
키 포인트
그리고 이것이 문제의 핵심 키포인트입니다. 건너건너 연결된 관계까지 모두 확인해야만 경기 결과 속에 숨어있는 모든 순위 관계를 파악할 수 있습니다. 그리고 이 과정에서 DFS가 사용됩니다.내가 이기는 상대가 이기는 상대가 이기는... 을 모두 파악해야 하기 때문입니다.
순위 확정 판별 조건
순위가 확정됐음은 어떻게 판별할 수 있을까요? 우선 모든 관계를 파악합니다. 그리고 n명의 선수들이 있을 때, 특정 선수가 이기는 선수 + 지는 선수 = (n-1)명이라면, 그 선수는 순위가 확정됐다고 판단할 수 있습니다. 그래프에서는, 한 node에서 들어오거나 나가는 edge의 수가 n-1인 node를 의미합니다 (건너건너 포함).
// 순위를 알 수 있는 선수의 수를 센다
for (i in 1..n){
if (edgeCount[i] == n-1) answer++
}
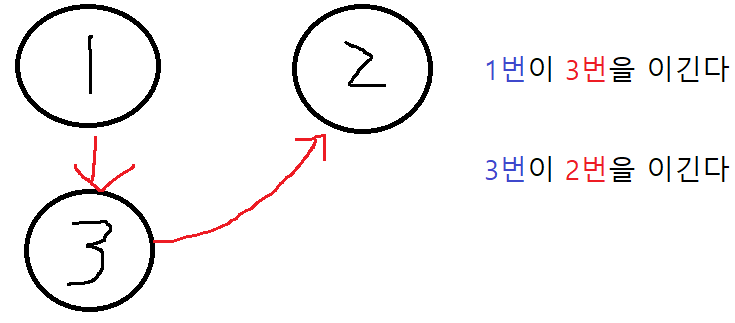
예를 들어, 1번이 3번을 이기고, 3번이 2번에게 이기면 3번의 입장만 고려했을 때, 3명 중 2명과의 관계를 알고 있으므로 순위가 확정된 것입니다.
DFS
DFS를 사용하여 각 선수마다 내가 이길 수 있는 모든 선수와 내가 지는 모든 선수를 알아냅니다. 그리고 몇 명인지만 알면 되기 때문에 문제는 더 간단해집니다.
각 노드를 시작 노드로 해서 이길 수 있는 모든 선수를 확인합니다. 그리고 그 과정에서 반대로 지는 선수는 그 시작 노드에게 진다는 체크를 해줍니다. 즉, 이기는 노드들에 대한 방문만을 통해 지는 정보까지 모두 알 수 있게 됩니다.
/*
* src: 이기는 선수 current: 지는 선수, loser: current에게 지는 선수
* src가 이길 수 있는 모든 선수를 DFS로 확인한다.
* 이 과정에서 반대로 current들은 src에게 진다는 정보도 알 수 있다.
*/
private fun countEdgesOf(src: Int, current: Int) {
for (loser in winList[current]) {
if (visited[src][loser]) continue
visited[src][loser] = true
// 관계가 n-1개인지만 확인하면 되기 때문에
// 이기고 지는 경우 상관없이 관계 개수를 카운팅한다.
count[src]++ // src가 loser를 이긴다
count[loser]++ // loser는 src에게 진다
countEdgesOf(src, loser) // 건너 관계를 확인한다.
}
}
위의 예를 다시 가져와 보겠습니다. [1, 3], [3, 2]가 입력으로 들어오고, 1에 대해 DFS를 시작합니다.
depth1) 1 -> 3
- 1이 3을 이긴다. (edgeCount[1]++;)
- 3이 1한테 진다. (edgeCount[3]++;)
1에서 3을 방문할 때 1에 대한 정보만이 아닌 3에 대한 정보도 확인할 수 있습니다. 또한, 엣지의 개수만 센다는 것에 주목해주세요. 실제로 필요한건 관계의 개수이기 때문입니다.
depth2) (1 ->) 3 -> 2
앞에 (1 ->)가 있습니다. 1에서부터 시작했다는 의미입니다.
1이 2를 이긴다. (edgeCount[1]++;)
2가 1한테 진다. (edgeCount[2]++;)
정답
이것을 모든 노드에 대해 실행한 후, edgeCount[i] == n-1인 개수를 세면 그것이 답이 됩니다.
코드
class Solution {
private lateinit var edgeCount: IntArray // 들어오거나 나가는 edge 개수
private lateinit var visited: Array<BooleanArray> // visited[src][dst]
private lateinit var winList: Array<MutableList<Int>> // [node]가 이긴 선수들
fun solution(n: Int, results: Array<IntArray>): Int {
var answer = 0
edgeCount = IntArray(n+1)
visited = Array(n+1){
BooleanArray(n+1)
}
winList = Array(n+1) {
mutableListOf<Int>()
}
results.forEach {
val winner = it[0]
val loser = it[1]
winList[winner].add(loser)
}
// 모든 관계를 확인한다
for (i in 1..n) {
countEdgesOf(i, i)
}
// 순위를 알 수 있는 선수를 센다
for (i in 1..n){
if (edgeCount[i] == n-1) answer++
}
return answer
}
/*
* src: 이기는 선수 current: 지는 선수, loser: current에게 지는 선수
* src가 이길 수 있는 모든 선수를 DFS로 확인한다.
* 이 과정에서 반대로 current들은 src에게 진다는 정보도 알 수 있다.
*/
private fun countEdgesOf(src: Int, current: Int) {
for (loser in winList[current]) {
if (visited[src][loser]) continue
visited[src][loser] = true
// 관계가 n-1개인지만 확인하면 되기 때문에
// 이기고 지는 경우 상관없이 관계 개수를 카운팅한다.
edgeCount[src]++ // src가 loser를 이긴다
edgeCount[loser]++ // loser는 src에게 진다
countEdgesOf(src, loser) // 건너 관계를 확인한다.
}
}
}'Problem Solving > 프로그래머스' 카테고리의 다른 글
| 프로그래머스: 프린터 (Kotlin) (0) | 2022.03.31 |
|---|---|
| (Java) 프로그래머스 - 아이템 줍기 (0) | 2022.03.12 |
| (Kotlin) 프로그래머스 - 표 편집 [2021 카카오 채용연계형 인턴십] (0) | 2022.01.07 |
| (Kotlin) 프로그래머스 - 오픈채팅방 [2019 KAKAO BLIND RECRUITMENT] (0) | 2021.08.23 |
| (Kotlin) 프로그래머스 - 키패드 누르기 [2020 카카오 인턴십] (0) | 2021.08.22 |