https://www.acmicpc.net/problem/1074
1074번: Z
한수는 크기가 2N × 2N인 2차원 배열을 Z모양으로 탐색하려고 한다. 예를 들어, 2×2배열을 왼쪽 위칸, 오른쪽 위칸, 왼쪽 아래칸, 오른쪽 아래칸 순서대로 방문하면 Z모양이다. N > 1인 경우, 배열을
www.acmicpc.net
풀이
같은 유형의 작은 문제들로 계속 쪼개어지는 것으로 보아, 분할 정복 문제라는 것을 알 수 있었다. 그치만 시간 제한이 0.5초라서 주의해야 할 부분이 있었다.
행렬 표현
먼저 탐색에 앞서 행렬은 시작점과 각 변의 길이를 통해 나타낼 수 있다.
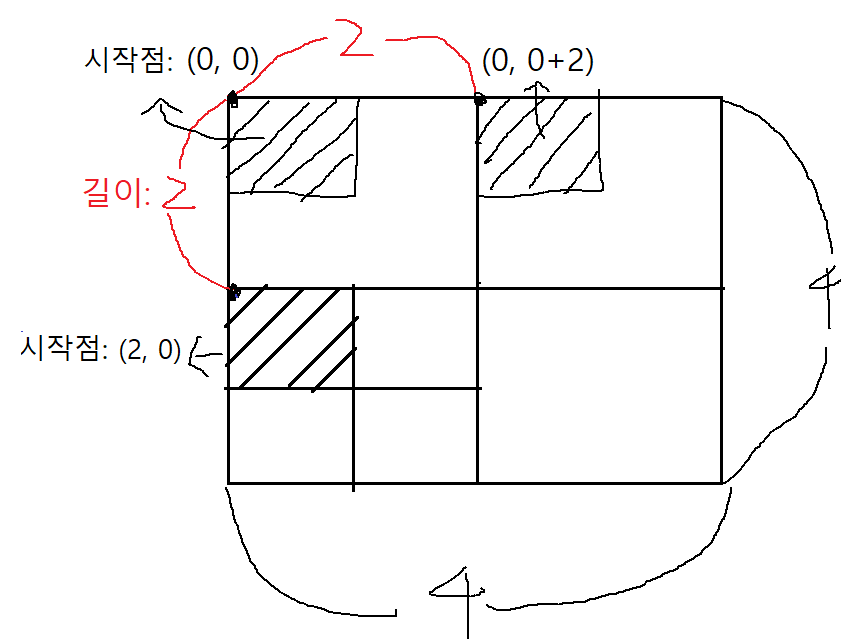
1. 시간 제한을 고려하지 않는 방법
- (0, 0)과 전체 크기의 행렬을 대상으로 탐색을 시작한다.
- 지금 탐색중인 행렬의 길이를 확인한다.
- 2보다 길거나 같으면, 길이를 2로 나눠서 Z모양에 따라 다시 재귀적으로 탐색한다.
- 길이가 1이고,
- 목표 지점이라면, 몇 번째로 방문했는지 저장하고 탐색을 종료한다.
- 목표 지점이 아니라면,해당 점의 위치를 확인하고 방문 순서(count)를 +1 증가시키고 재귀 탐색을 종료한다.
- 목표점의 방문 순서를 출력한다.
이렇게 하면 항상 정답을 찾을 수 있다. 하지만 코드를 제출해보면 시간 초과가 발생한다.
📌시간 복잡도)
- (2^n * 2^n) 행렬의 길이가 1(한 점)이 될 때까지 2로 나누는 횟수 = log(2^n) = n
- 모든 점의 개수 = 2^n * 2^n
연산 횟수: (2^n * 2^n) * n = 2^15 * 2^ 15 * 15 = 약 160억
시간 복잡도: O(n*4^n)
따라서, 연산 횟수를 줄여야 한다. 그리고 아래의 그림과 같이 찾는 점이 존재하는 구간만 재귀적으로 탐색하면 시간 복잡도를 확 줄일 수 있다. 나머지 부분은 방문 순서만 업데이트 해준다.
2. 시간 복잡도를 개선한 방법
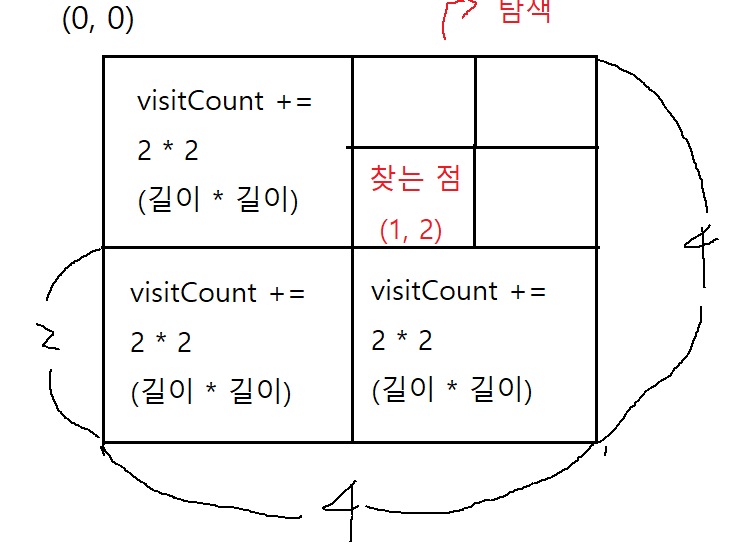
- (2^n * 2^n) 행렬을 Z모양의 순서대로 탐색한다.
- 지금 탐색중인 범위가 내가 찾으려고 하는 최종 범위(점)인지 확인한다.
- 찾던 점이라면, 몇 번째로 방문했는지 저장한다.
- 아니라면, Z방향 순서대로
- 목표지점을 포함하지 않는 곳은 방문 순서(visitCount)만 길이 * 길이만큼 증가시키고 탐색을 종료한다
- 목표지점을 포함하는 곳은 길이를 절반으로 나눠서 탐색을 계속한다.
- 목표점의 방문 순서를 출력한다.
📌줄어든 시간 복잡도)
- 필요한 점을 찾기 위해 구간을 나누는 횟수 = log(2^n) = n,
- 나눌 때마다 방문 순서 업데이트 하는 연산 횟수 3번
연산 횟수: 3 * n = 3 * 15 = 45
시간 복잡도: O(n)
코드
import java.io.BufferedReader
import java.io.InputStreamReader
var answer = 0
var numbering = 0
// dudwls901님 풀이 참고 버전
fun main() = with(BufferedReader(InputStreamReader(System.`in`))) {
val input = readLine().split(" ").map{ it.toInt() }
val (n, r, c) = input
visitGraph(1 shl(n), 0, 0, r, c)
print(answer)
}
fun visitGraph(size: Int, row: Int, col: Int, targetRow: Int, targetCol: Int) {
// 탐색중인 Z구간에 목표지점이 없으면
// 탐색하지 않고 방문 순서만 update하고 탐색을 종료한다
if (targetRow !in row until row + size || targetCol !in col until col + size) {
numbering += size * size
return
}
// 목표지점을 찾았으면 방문 순서를 저장하고 리턴한다
if (row == targetRow && col == targetCol) {
answer = numbering
return
}
val halfSize = size / 2
visitGraph(halfSize, row, col, targetRow, targetCol) // 왼쪽 위
visitGraph(halfSize, row, col + halfSize, targetRow, targetCol) // 오른쪽 위
visitGraph(halfSize, row + halfSize, col, targetRow, targetCol) // 왼쪽 아래
visitGraph(halfSize, row + halfSize, col + halfSize, targetRow, targetCol) // 오른쪽 아래
}'Problem Solving > 백준' 카테고리의 다른 글
| 백준 1451번: 직사각형으로 나누기 (Kotlin) (0) | 2022.01.11 |
|---|---|
| 백준 1170번: 리모컨 (Kotlin) (0) | 2022.01.09 |
| 백준 1783번: 병든 나이트 (Kotlin) (0) | 2022.01.06 |
| 백준 1517번: 버블 소트 (Kotlin) (0) | 2022.01.05 |
| 백준 2447번: 별 찍기 - 10 (Kotlin) (0) | 2021.12.31 |