https://www.acmicpc.net/problem/1517
1517번: 버블 소트
첫째 줄에 N(1 ≤ N ≤ 500,000)이 주어진다. 다음 줄에는 N개의 정수로 A[1], A[2], …, A[N]이 주어진다. 각각의 A[i]는 0 ≤ |A[i]| ≤ 1,000,000,000의 범위에 들어있다.
www.acmicpc.net
풀이
크게 2가지의 풀이 법이 있다. 그 중 좀 더 쉬운 방법이 분할 정복법인데, 그것도 아이디어를 떠올리기가 쉽지 않은 것 같다. 그래서 다른 분들의 풀이와 코드를 많이 참고했다.
먼저, 수가 최대 50만개라서 버블 소트를 쓰면 시간 초과가 난다.
각 숫자가 몇 번 swap 되는지를 그림으로 알아보면 다음과 같다.
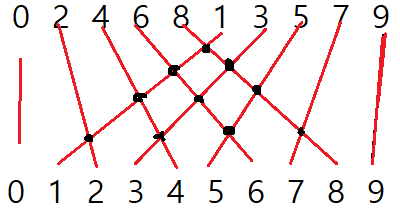
각 숫자의 교점의 합이 총 swap의 합이 된다. 그리고 각 숫자의 교점의 개수는 자신보다 오른쪽에 있는 숫자들 중 더 작은 수의 개수가 된다. 예를 들어, 위의 6은 1, 3, 5 => 3번 swap 한다.
그러면 어떻게 O(n^2)보다 빠르게 각 숫자들의 오른쪽을 탐색할 수 있을까? Merge Sort를 하면 merge sort의 시간 복잡도인 O(n * log^n) 안에 가능하다.

위의 그림은 merge sort를 하는 과정에서 가장 작은 0을 정렬한 다음 상황이다.
이제 왼쪽에서 가장 작은 2와 오른쪽에서 가장 작은 1 중 더 작은 값을 정렬해야 한다. 오른쪽 값이 더 작기 때문에 1을 정렬한다. 그리고 그 과정에서 1이 2,4,6,8과 교차되는 것을 알 수 있다. 즉, 1은 2, 4, 6, 8과 swap이 되고, swap += (왼쪽 배열 개수 - 왼쪽 인덱스)와 같은 방식으로 swap 횟수를 계산할 수 있다. 이러한 과정은 오른쪽 최소 값이 왼쪽 최소값보다 작을 때마다 적용된다.
참고로 swap 횟수는 최악의 경우 대략 50만 + ... + 1 => 50만 * 50만이 될 수 있기 때문에 Long형을 사용해야 한다!
코드
import java.io.BufferedReader
import java.io.InputStreamReader
import java.util.*
var count = 0L
lateinit var tempArray: IntArray
fun main() = with(BufferedReader(InputStreamReader(System.`in`))) {
val n = readLine().toInt()
val st = StringTokenizer(readLine())
val numbers = IntArray(n) { i ->
st.nextToken().toInt()
}
tempArray = IntArray(n)
mergeSort(numbers, 0, n-1)
print(count)
}
fun mergeSort(numbers: IntArray, start: Int, end: Int) {
if (start == end) {
return
}
val mid = (start + end) / 2
mergeSort(numbers, start, mid)
mergeSort(numbers, mid + 1, end)
merge(numbers, start, end) // 정렬된 양쪽 배열을 합치면서 다시 정렬한다
}
fun merge(numbers: IntArray, start: Int, end: Int) {
val mid = (start + end) / 2
var left = start
var right = mid + 1
var tempIndex = start
while(left <= mid && right <= end) {
// 꼭 등호는 왼쪽이 더 작거나 같은 조건으로 붙여야 한다.
// 그렇지 않으면 왼쪽과 오른쪽 값이 같을 때 1을 더 계산하게 된다.
if (numbers[left] <= numbers[right]){
// 왼쪽 값이 더 작거나 같다 -> 오른쪽 배열에 자신보다 큰 값이 없다
tempArray[tempIndex++] = numbers[left++]
}else{
tempArray[tempIndex++] = numbers[right++]
count += mid - left + 1
}
}
// 왼쪽이나 오른쪽 중 남아있는 배열의 숫자 정렬
while (left <= mid) {
tempArray[tempIndex++] = numbers[left++]
}
while (right <= end) {
tempArray[tempIndex++] = numbers[right++]
}
// 임시 배열에 정렬한 값을 원래 배열에 반영
for (i in start..end) {
numbers[i] = tempArray[i]
}
}'Problem Solving > 백준' 카테고리의 다른 글
| 백준 1074번: Z (Kotlin) (0) | 2022.01.07 |
|---|---|
| 백준 1783번: 병든 나이트 (Kotlin) (0) | 2022.01.06 |
| 백준 2447번: 별 찍기 - 10 (Kotlin) (0) | 2021.12.31 |
| 백준 1780번: 종이의 개수 (Kotlin) (0) | 2021.12.30 |
| 백준 1654번: 랜선 자르기 (Kotlin) (0) | 2021.12.27 |