https://www.acmicpc.net/problem/2225
2225번: 합분해
첫째 줄에 답을 1,000,000,000으로 나눈 나머지를 출력한다.
www.acmicpc.net
풀이
이전 항으로 다음 항의 값을 구할 수 있는 다이나믹 프로그래밍 문제이다.
문제의 상황을 수식으로 나타내보면 다음과 같다.
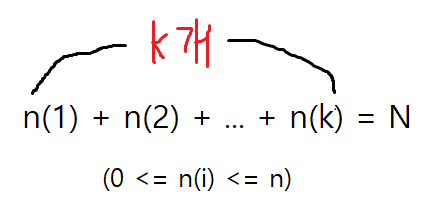
이렇게 되는 경우의 수를 dp[k][N]이라고 할 떄, 위에 수식은 아래처럼 다시 바꿔서 표현할 수 있다.
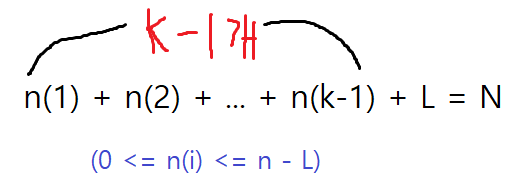
L이라는 값을 미리 더해서 (0 ~ n-L)까지 k-1개의 숫자를 더해서 N-L을 만드는 경우의 수를 구하는 상황으로 바꿀 수 있고, k-1개로 묶인 부분이 dp[k-1][N-L]이 된다.
그러면 dp[k][N] = sum( dp[k-1][N-L] ) (0 <= L <= N)이라는 점화식을 만들어낼 수 있는데, 변수가 3개이므로 3중 반복문을 사용해서 구현할 수 있다.
dp[k][N]의 식을 조금 살펴보면,
k = 1일 때 즉, 숫자 하나로 N을 만드는 경우의 수는 N이 무엇이든 항상 N 하나이므로 dp[1][N] = 1이다. 그리고 이게 초기 값이 된다.
n =0일 때는 숫자가 몇 개든지 0만 더해지는 경우밖에 없다. 따라서 dp[k][0] = 1이다.
ex) dp[4][0] = 1 (0 + 0 + 0 +0)
그리고 이것들이 dp의 초기 값이 된다.
머리로만 하면 이해가 잘 안될 수도 있어서 직접 해보는 게 좋다. 내가 그랬다ㅋ_ㅋ
ex) n = 6, k = 4일 때 반복문 결과
| dp[k][n] | n = 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| k =1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 1+1=2 | 1+1+1=3 | 4 | 5 | 6 | 7 |
| 3 | 1 | 1+2=3 | 1+2+3=6 | 10 | 15 | 21 | 28 |
| 4 | 1 | 1+3=4 | 1+3+6=10 | 20 | 35 | 56 | 56+28=84 |
계산하다 보면 dp[k][n] = dp[k][n-1] + dp[k-1][n] 이라는 특이한 구조를 발견할 수 있다. 이 점화식을 사용하면 변수가 두 개라서 이중반복문으로 좀 더 빠르게 구현이 가능하다!
삼중반복문이 처음엔 머리에 잘 안들어왔었는데, 직접 해보는게 이해에 도움이 많이 됐던 문제다.
코드1 (삼중 반복문)
fun main(){
val input = readLine()!!.trim().split(" ")
var n = input[0].toInt()
var k = input[1].toInt()
val dp = Array(k+1){IntArray(n+1)}
for (i in 0..n) dp[1][i] = 1
for (i in 2..k){ // 행: 더하는 숫자 개수
for (j in 0..n){ // 열: 더해서 나와야 하는 값
for (m in 0..j){
dp[i][j] += dp[i-1][j - m] // 직전 행의 처음~현재 열까지 더한다.
dp[i][j] %= 1_000_000_000
}
}
}
println(dp[k][n])
}
코드2 (재귀)
lateinit var dp: Array<IntArray>
fun main() {
val input = readLine()!!.trim().split(" ")
var n = input[0].toInt()
var k = input[1].toInt()
dp = Array(k+1){IntArray(n+1)}
for (i in 0..n){
dp[1][i] = 1 // 더하는 숫자가 하나일 때
}
println(findAnswer(n, k))
}
private fun findAnswer(n: Int, k:Int): Int {
if (dp[k][n] != 0) return dp[k][n]
for (i in 0..n){
dp[k][n] += findAnswer(n-i, k-1)
dp[k][n] %= 1_000_000_000
}
return dp[k][n]
}
코드3 (이중 반복문)
fun main(){
val input = readLine()!!.trim().split(" ")
var n = input[0].toInt()
var k = input[1].toInt()
val dp = Array(k+1){IntArray(n+1)}
for (i in 1..k) dp[i][0] = 1 // 합한 값이 0인 경우는 항상 한 가지이다
for (i in 1..n) dp[0][i] = 0 // dp[1][i] = 1로 세팅하고, 반복문을 2..k으로 시작하는 거랑 같음
for (i in 1..k){
for (j in 1..n){
dp[i][j] = dp[i][j-1] + dp[i-1][j]
dp[i][j] %= 1_000_000_000
}
}
println(dp[k][n])
}'Problem Solving > 백준' 카테고리의 다른 글
| 백준 9466번: 텀 프로젝트 (Kotlin) (0) | 2021.12.22 |
|---|---|
| 백준 1406번: 에디터 (Kotlin) (0) | 2021.12.16 |
| 백준 2075번: N번째 큰 수 (Kotlin) (0) | 2021.12.12 |
| 백준 19598번: 최소 회의실 개수 (Kotlin) (0) | 2021.12.11 |
| 백준 2579번: 계단 오르기 (Kotlin) (0) | 2021.12.08 |