https://www.acmicpc.net/problem/1451
1451번: 직사각형으로 나누기
첫째 줄에 직사각형의 세로 크기 N과 가로 크기 M이 주어진다. 둘째 줄부터 직사각형에 들어가는 수가 가장 윗 줄부터 한 줄에 하나씩 M개의 수가 주어진다. N과 M은 50보다 작거나 같은 자연수이
www.acmicpc.net
난 아무래도 기하랑 도형에 약한 것 같다. 어려웠다..ㅋㅋ 도형만 나오면 시야가 좁아진다.
처음에 직사각형 중 3개의 작은 직사각형의 합의 곱이라고 이해하고, '한 두 개 점을 포함하지 않으면서 최대로 직사각형을 3개 만들 수 있는 방법도 있지 않을까' 싶었다. 상식적으론 모든 점을 다 포함해야 최대 값이 나올 것 같았지만, 수학의 세계는 혹시 모르니까..
어떻게 하는 걸까 고민하다가 다시 확인해보니 직사각형을 3개로 분할하는 문제였다.
풀이
직사각형을 3개로 분할할 수 있는 모양은 6가지가 있다.

이 각각의 형태에 대해 모든 크기를 확인해보면 최대값을 구할 수 있다.
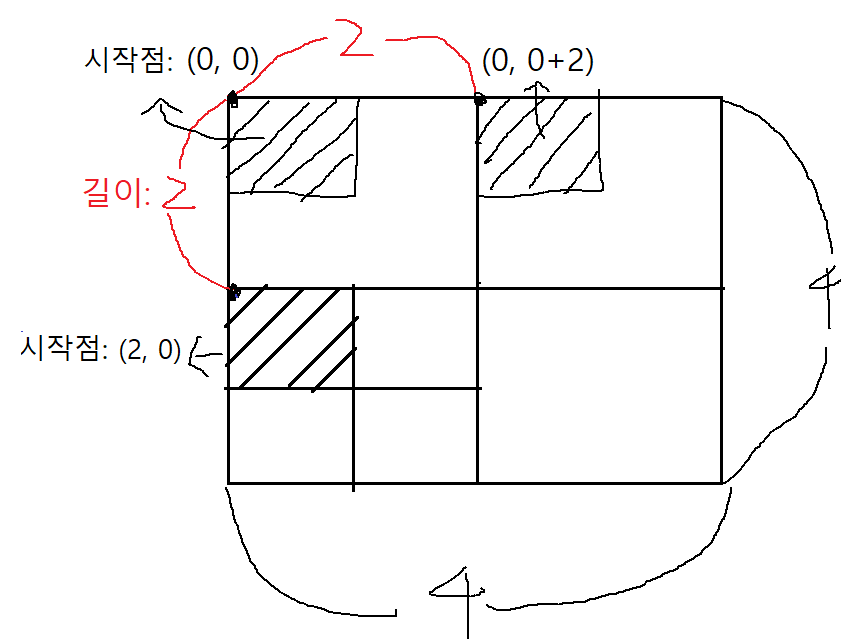
행렬을 표현하는 방법으로는 크게 2가지가 있다. (1) 한 점과 가로,세로 길이로 표현하는 방법과 (2)왼쪽 상단과 오른쪽 하단과 같이 양 끝의 두 점으로 표현하는 방법이다. 개인적으로 정사각형일 땐 (1)이 편하고 직사각형은 (2)가 편했다.
ex) 4번째 모양


이런 식으로 구성하면 한 줄짜리 행렬처럼 해당 모양을 만들 수 없을 땐, 반복문의 start, end 크기가 역전돼서 자동적으로 반복문이 실행되지 않는다.
코드
import java.io.BufferedReader
import java.io.InputStreamReader
import java.util.*
import kotlin.math.max
fun main() = with(BufferedReader(InputStreamReader(System.`in`))) {
val input = readLine().split(" ")
val rowSize = input[0].toInt()
val colSize = input[1].toInt()
val square = Array<IntArray>(rowSize) {
val numbers = readLine()
IntArray(colSize) { i ->
numbers[i] - '0'
}
}
val lastRowIdx = rowSize - 1
val lastColIdx = colSize - 1
var answer = 0L
// III
for (col1 in 0 until colSize - 2) {
for (col2 in col1+1 until colSize - 1) {
val sum1 = getSquareSum(square, 0, 0, lastRowIdx, col1)
val sum2 = getSquareSum(square, 0, col1+1, lastRowIdx, col2)
val sum3 = getSquareSum(square, 0, col2+1, lastRowIdx, lastColIdx)
answer = max(answer, sum1 * sum2 * sum3)
}
}
// =
for (row1 in 0 until rowSize - 2) {
for (row2 in row1 + 1 until rowSize - 1) {
val sum1 = getSquareSum(square, 0, 0, row1, lastColIdx)
val sum2 = getSquareSum(square, row1+1, 0, row2, lastColIdx)
val sum3 = getSquareSum(square, row2+1, 0, lastRowIdx, lastColIdx)
answer = max(answer, sum1 * sum2 * sum3)
}
}
// ㅜ
for (row in 0 until rowSize - 1) {
val sum1 = getSquareSum(square, 0, 0, row, lastColIdx)
for (col in 0 until colSize - 1) {
val sum2 = getSquareSum(square, row+1, 0, lastRowIdx, col)
val sum3 = getSquareSum(square, row+1, col+1, lastRowIdx, lastColIdx)
answer = max(answer, sum1 * sum2 * sum3)
}
}
// ㅗ
for (row in lastRowIdx downTo 1) {
val sum1 = getSquareSum(square, row, 0, lastRowIdx, lastColIdx)
for (col in 0 until colSize - 1) {
val sum2 = getSquareSum(square, 0, 0, row-1, col)
val sum3 = getSquareSum(square, 0, col+1, row-1, lastColIdx)
answer = max(answer, sum1 * sum2 * sum3)
}
}
// ㅏ
for (col in 0 until colSize - 1) {
val sum1 = getSquareSum(square, 0, 0, lastRowIdx, col)
for (row in 0 until rowSize - 1) {
val sum2 = getSquareSum(square, 0, col+1, row, lastColIdx)
val sum3 = getSquareSum(square, row+1, col+1, lastRowIdx, lastColIdx)
answer = max(answer, sum1 * sum2 * sum3)
}
}
// ㅓ
for (col in lastColIdx downTo 1) {
val sum1 = getSquareSum(square, 0, col, lastRowIdx, lastColIdx)
for (row in 0 until rowSize - 1) {
val sum2 = getSquareSum(square, 0, 0, row, col-1)
val sum3 = getSquareSum(square, row+1, 0, lastRowIdx, col-1)
answer = max(answer, sum1 * sum2 * sum3)
}
}
print(answer)
}
fun getSquareSum(square: Array<IntArray>, startRow: Int, startCol: Int, endRow: Int, endCol: Int): Long {
var sum = 0L
for (row in startRow..endRow) {
for (col in startCol..endCol) {
sum += square[row][col]
}
}
return sum
}
'Problem Solving > 백준' 카테고리의 다른 글
| 백준 22862번: 가장 긴 짝수 연속한 부분 수열 (large) (Kotlin) (0) | 2022.01.14 |
|---|---|
| 백준 1697번: 숨바꼭질 (Kotlin) (0) | 2022.01.11 |
| 백준 1170번: 리모컨 (Kotlin) (0) | 2022.01.09 |
| 백준 1074번: Z (Kotlin) (0) | 2022.01.07 |
| 백준 1783번: 병든 나이트 (Kotlin) (0) | 2022.01.06 |