개발해요

https://www.acmicpc.net/problem/11509

안녕하세요, 이륙사입니다. 이번 게시물에서는 풍선 맞추기 문제의 풀이 과정을 복기하며 기록했습니다. 백준에서 그리디 알고리즘이라고 나와있지만, 개인적으로는 어떻게 단일 반복문으로 해결할 수 있을까에 대한 구현 문제에 가깝다고 느꼈습니다.

풀이 과정

먼저, 최소한의 화살을 사용하기 위해선 하나의 화살로 최대한 많은 풍선을 터뜨려야 합니다.

화살은 풍선을 하나 맞힐 때마다 높이가 1씩 감소하므로, 내림차순으로 높이가 1 차이나는 풍선들은 높이가 가장 큰 풍선에 화살을 한번 쏘는 것으로 그 풍선들을 모두 맞힐 수 있습니다. 

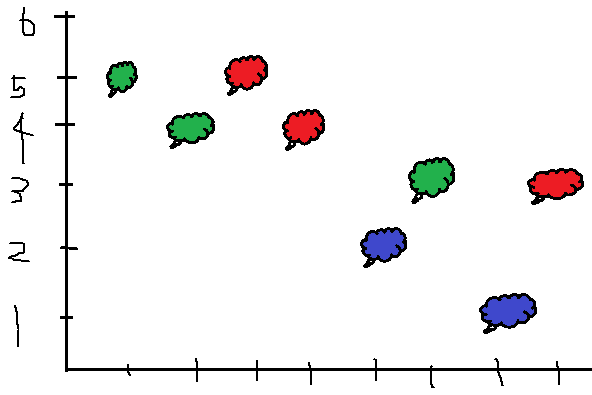
위의 예시의 경우, 3개의 화살(화살1(5, 4, 3), 화살2(5, 4, 3), 화살3(2, 1))로 풍선들을 전부 맞힐 수 있습니다.

접근

저는 먼저 이중 반복문으로 완전 탐색하는 방법을 떠올렸습니다. 앞에 있는 풍선에 화살을 쏘고, 뒤에 그 화살로 제거할 수 있는 풍선들이 있는지 확인하는 것입니다. 그럴려면 이중 반복문을 사용해야 하는데, 풍선이 최대 100만개라서 이 방법으론 시간 내에 해결이 불가능했습니다.

단일 반복문으로 줄일 수 있을까 고민하다가, 이중 반복문을 사용해도 날아가는 화살의 높이를 알고 있어야 한다는 점에 주목했습니다. 반복문으로 풍선들을 확인할 때 이때까지 쏜 화살 중 현재 확인하는 풍선의 높이로 날아오고 있는 화살이 있으면 쏘지 않고(저장x), 없으면 새로 쏘면 되겠다. 즉, 해싱(or 인덱스: 풍선 높이, 원소: 화살 개수)을 사용하면 단일 반복문으로 해결할 수 있겠다고 생각했습니다. 

val arrows = IntArray(MAX_HEIGHT + 1) // 날아가고 있는 화살을 높이에 따라 저장

balloons.forEach { height ->
    if (arrows[height] == 0) {  // height 높이에 날아오는 화살이 없으면
        count += 1              // 쏜다
        arrows[height - 1] += 1 // 풍선에 맞고 화살 높이 감소
    } else if (arrows[height] > 0) { // 날아오는 화살이 있으면
        arrows[height] -= 1          // 풍선에 맞는다
        arrows[height - 1] += 1
    }
}

코드

import java.io.BufferedReader
import java.io.InputStreamReader
import java.util.*

const val MAX_HEIGHT = 1_000_000

fun main() = with(BufferedReader(InputStreamReader(System.`in`))) {
    val n = readLine().toInt()
    val st = StringTokenizer(readLine())
    val balloons = IntArray(n) {
        st.nextToken().toInt()
    }
    var count = 0
    val arrows = IntArray(MAX_HEIGHT + 1) // 날아가고 있는 화살을 높이에 따라 저장

    balloons.forEach { height ->
        if (arrows[height] == 0) {  // height 높이에 날아오는 화살이 없으면
            count += 1              // 쏜다
        } else if (arrows[height] > 0) { // 날아오는 화살이 있으면
            arrows[height] -= 1          // 풍선에 맞는다
        }

        arrows[height - 1] += 1 // 풍선에 맞고 화살 높이 감소
    }

    print(count)
}

https://www.acmicpc.net/problem/13164

안녕하세요, 이륙사입니다.

풀이

위 문제는 비용이 키 차이와 관련있다는 사실에서부터 시작하는 문제였습니다.

인접한 원생들의 키 차이를 값으로 갖는 새로운 수열을 구합니다. 그리고 그 수열의 합에서 값이 가장 큰 k-1개의 값을 빼면 그것이 정답이 됩니다. 왜냐하면 (큰 키 - 작은 키)의 값은 그 사이에 있는 원생들간 키 차이의 합과 같기 때문입니다. 그리고 아래 예시처럼 조를 k개로 나누면 k-1개의 경계가 생기며, 그 경계에 해당하는 차이 값들만 비용을 계산하는데 사용되지 않습니다. 따라서, 전체 차이의 합에서 가장 큰 k-1개를 빼주면 그것이 답이 됩니다.

예)

7, 3

1 3 5 6 10 16 19

또한, 전체 값의 합에서 가장 큰 값들을 빼주기 때문에 그리디 유형의 문제라고 할 수 있습니다. 

생각 과정

1. 학생 수가 최대 300,000이므로, 전부 확인해볼 순 없다.
2. 비용은 조에서 가장 키가 큰 학생과 가장 작은 학생의 차이다 --> 값의 차이에 주목한다.
3. 인접 원소들간 차이에 대해서도 생각해볼 수 있다.
4. 가장 키가 큰 학생과 작은 학생의 키 차이는 두 학생 사이에 있는 학생들간 키 차이의 합이란 것을 발견한다.
5. 조를 나누어본 결과, 비용의 합은 전체 키 차이의 합에서 가장 큰 k-1개의 값을 뺀 값이라는 것을 확인한다.

코드

import java.io.BufferedReader
import java.io.InputStreamReader
import java.util.*
import kotlin.math.sqrt

fun main() = with(BufferedReader(InputStreamReader(System.`in`))) {
    val (n, k) = readLine().split(" ").map{ it.toInt() }
    val st = StringTokenizer(readLine())
    val gaps = IntArray(n) { st.nextToken().toInt() }
    
    // 인접 학생간 키차이를 값으로 갖는 수열
    for (i in 0 until n-1) {
        gaps[i] = gaps[i+1] - gaps[i]
    }

    // k개로 나누면 k-1개의 경계가 생긴다
    gaps.sort() // 전체에서 값이 큰 경계 k-1개를 빼기 위해 먼저 정렬한다  
    
    // 가장 큰 k-1개를 뺀 나머지를 모두 더한다
    val min = (0 until (n-1)-(k-1)).sumOf { i -> gaps[i] }
    print(min)
}