https://www.acmicpc.net/problem/1167
1167번: 트리의 지름
트리가 입력으로 주어진다. 먼저 첫 번째 줄에서는 트리의 정점의 개수 V가 주어지고 (2 ≤ V ≤ 100,000)둘째 줄부터 V개의 줄에 걸쳐 간선의 정보가 다음과 같이 주어진다. 정점 번호는 1부터 V까지
www.acmicpc.net
풀이
트리에서 임의의 두 노드 거리 중 가장 긴 것을 구하는 문제이지만 예시랑 설명이 부족하다. 1967번(https://www.acmicpc.net/problem/1967)이랑 비슷해서 그런 거 같은데, 이 문제의 예시를 살펴보는 걸 추천한다!
트리의 지름을 구하는 문제는 공식처럼 증명된 방법(https://blog.myungwoo.kr/112)이 있는데 그 외의 방법을 이야기 해보려고 한다.
임의의 두 노드 사이의 거리를 구하는 방법을 찾아내기 위해, 특정 노드를 포함하는 최장 거리를 살펴보면 다음과 같다.

노드1을 포함하는 가장 긴 경로는 8-4-2-(1)-3-5-9로, 7+5+3+2+11+15 = 43이 된다. 그럼 전체 트리의 지름은 무엇일까?

9-5-(3)-5-12 -> 15+11+9+10 = 45로, 루트1을 포함하지 않는 것을 알 수 있다. 그럼, 트리의 지름과 루트 노드는 관련이 없는 것 같은데, 사실은 매우 관련이 있다.
1967번 문제 설명에서 알 수 있듯이, 트리의 지름은 경로를 포함하는 양 끝점을 양방향으로 잡아당겼을 때의 가장 긴 거리라고도 생각할 수 있다. 이것을 루트 노드와 결합해서 생각해보면 다음과 같다.
"각 점을 루트로 하는 서브 트리에서, 각 자식 노드에서 leaf 노드까지 가는 경로 중 가장 긴 경로의 합"
그림과 함께 설명하면 다음과 같다.

노드1을 루트로 하는 트리에서, 각 자식 노드(노드2, 노드3)에서 leaf 노드로 가는 경로는 6개이다.
1 -> 2~7
1 -> 2~8
1 -> 3~9
1 -> 3~10
1 -> 3~11
1 -> 3~12
여기서 2에서 가는 경로 중 최장 거리 하나와 3에서 가는 최장 거리를 하나씩 선택하면, 양 방향 잡아당겼을 때 최장 거리가 된다.
그리고 이것을 임의로 노드의 지름이라고 하면, 각 노드그의 지름 중 최대 값이 전체 트리의 지름이 된다. 왜냐하면 트리는 사실 어떤 노드도 루트가 될 수 있기 때문이다.
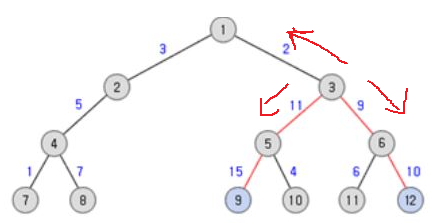
그래서 위 그림에서의 전체 지름도 (3 -> 1~), (3 -> 5~), (3 -> 6 ~)의 경로 중 가장 긴 2개를 더한 값이 답이 된 것이다.
구현 방법 (DFS)
1. 트리를 입력받는다
2. 루트 -> 자식 하나의 최장 거리를 반환하는 함수를 재귀로 작성한다.
2-1) 재귀 함수 안에서 루트의 인접 노드를 대상으로 반복문을 돌린다.

2-2) 반복문 안에서 최장 거리를 구할 때마다 최대 값과 두 번째 최대 값을 갱신한다.

2-3) 모든 인접 노드를 탐색 후, 리턴하기 전에 지금까지 구한 지름과 (최대 값 + 두 번째 최대 값)을 비교해서 갱신한다.

참고한 곳 & 후기)
https://kimyunseok.tistory.com/125
개인적으로 재귀 구현이 어렵게 느껴질 때가 종종 있었는데, 재귀를 공부하는 데 많은 도움이 된 것 같다.
코드 1
import java.io.BufferedReader
import java.io.InputStreamReader
import java.util.*
import kotlin.math.max
data class Edge(var node: Int, var distance: Int)
var answer = 0
fun main() = with(BufferedReader(InputStreamReader(System.`in`))) {
val n = readLine().toInt()
val tree = Array(n+1){ mutableListOf<Edge>() }
// 트리 입력
repeat(n){
val st = StringTokenizer(readLine())
val node = st.nextToken().toInt()
var adjacentNode = st.nextToken().toInt()
while(adjacentNode != -1){
val distance = st.nextToken().toInt()
tree[node].add(Edge(adjacentNode, distance))
tree[adjacentNode].add(Edge(node, distance))
adjacentNode = st.nextToken().toInt()
}
}
val visited = BooleanArray(n+1).apply{ this[1] = true }
getMaxLengthFrom(tree, 1, visited) // 지름을 찾는다
print(answer)
}
// 루트에서 리프 노드까지 중 최장 거리를 구한다
fun getMaxLengthFrom(tree: Array<MutableList<Edge>>, rooteNode: Int, visited: BooleanArray): Int {
val edgeList = tree[rooteNode]
var firstMax = 0 // 리프 노드까지 가는 가장 긴 거리
var secondMax = 0 // 2번째로 긴 거리
// 인접 노드 리스트
for (i in edgeList.indices){
val adjacentNode = edgeList[i].node
if (visited[adjacentNode]) {
continue
}
visited[adjacentNode] = true
// 인접 자식까지 거리 + 자식에서 손자까지 최장거리
val maxLength = getMaxLengthFrom(tree, adjacentNode, visited) + edgeList[i].distance
// 최대 값 갱신
if (firstMax < maxLength){
secondMax = firstMax
firstMax = maxLength
}else if (secondMax < maxLength){
secondMax = maxLength
}
}
// 각 노드를 루트로하는 (가장 긴 거리 + 2번째로 가장 긴 거리)가 지름의 후보가 된다
answer = max(answer, firstMax + secondMax) // answer 값 갱신
return firstMax
}
코드 2 (공식)
import java.io.BufferedReader
import java.io.InputStreamReader
import java.util.*
data class Node(var node: Int, var distance: Int)
fun main() = with(BufferedReader(InputStreamReader(System.`in`))) {
val n = readLine().toInt()
val tree = Array(n+1) { mutableListOf<Node>() }
initTree(this, tree, n) // 트리 입력
val distance = IntArray(n+1){ -1 }.apply{ this[1] = 0} // 노드1과의 거리 + 중복 방문 체크 역할
findDiameter(distance, tree, 1) // 노드 1의 지름을 구한다
var tempDiameterNode = 0 // 노드1의 최장 노드
var tempMaxDistance = 0 // 노드1에서의 최장 거리
for (i in 1..n) {
if (tempMaxDistance < distance[i]){
tempMaxDistance = distance[i]
tempDiameterNode = i
}
}
// 거리 초기화
distance.apply {
for (i in 1..n) this[i] = -1
this[tempDiameterNode] = 0
}
findDiameter(distance, tree, tempDiameterNode) // 트리 지름 탐색
print(distance.maxOrNull())
}
fun initTree(br: BufferedReader, tree: Array<MutableList<Node>>, size: Int){
repeat(size) {
val st = StringTokenizer(br.readLine())
val node = st.nextToken().toInt()
var toNode = st.nextToken().toInt() // 인접 노드
while (toNode != -1) {
val distance = st.nextToken().toInt()
tree[node].add(Node(toNode, distance)) // 인접 리스트에 추가
toNode = st.nextToken().toInt() // 인접 노드 or -1
}
}
}
fun findDiameter(distance: IntArray, tree: Array<MutableList<Node>>, node: Int) {
val list = tree[node]
list.forEach { nextNode ->
if (distance[nextNode.node] == -1){
distance[nextNode.node] = distance[node] + nextNode.distance
findDiameter(distance, tree, nextNode.node)
}
}
}'Problem Solving > 백준' 카테고리의 다른 글
| 백준 1780번: 종이의 개수 (Kotlin) (0) | 2021.12.30 |
|---|---|
| 백준 1654번: 랜선 자르기 (Kotlin) (0) | 2021.12.27 |
| 백준 2146번: 다리 만들기 (Kotlin) (0) | 2021.12.24 |
| 백준 7576번: 토마토 (Kotlin) (0) | 2021.12.23 |
| 백준 9466번: 텀 프로젝트 (Kotlin) (0) | 2021.12.22 |