https://www.acmicpc.net/problem/2146
2146번: 다리 만들기
여러 섬으로 이루어진 나라가 있다. 이 나라의 대통령은 섬을 잇는 다리를 만들겠다는 공약으로 인기몰이를 해 당선될 수 있었다. 하지만 막상 대통령에 취임하자, 다리를 놓는다는 것이 아깝다
www.acmicpc.net
풀이
바다와 육지로 이루어진 인접 행렬 형태의 그래프가 주어진다. 그러면 모든 섬들을 찾아서, 그 섬들을 잇는 다리 중 가장 짧은 다리를 찾는 문제이다.
1. 섬 분류)
섬을 찾기 위해, 붙어있는 육지들을 하나로 묶어서 라벨링을 할 수 있다. 육지 한 점을 시작으로 인접한 곳을 탐색해 나가면서 인접한 곳에는 모두 같은 번호를 붙인다. dfs나 bfs를 사용할 수 있다.

2. 다리 연결)
방법 1) 모든 육지에서부터 한 번씩 경로를 탐색한다
이 부분이 까다로운데, 가장 쉽게 생각할 수 있는 방법은 모든 육지를 시작 지점으로 bfs를 수행하는 것이다. 너비 우선으로 탐색하기 때문에 시작 지점과 다른 섬의 육지에 처음 방문하게 됐을 때, 그 이동 거리가 그 지점에서 다른 섬으로 가는 최단 거리가 된다. 모든 지점에서 다른 섬으로 가는 최단 거리를 구하면, 그 중 최소값이 전체에서 가장 짧은 다리가 된다.
dfs를 사용하면 어떤 방향을 우선 탐색하느냐에 따라 아래처럼 돌아가는 경로를 먼저 탐색할 수 있다. 그래서 모든 점을 방문해야 하기 때문에 bfs를 사용하는 것이 좋다.

시간복잡도는 라벨링 O(n) + 경로 탐색 O(n^3) = O(n^3)이지만, n이 100이라서 괜찮다.
방법 2) 육지를 모두 Queue에 넣고, 한 번만 bfs를 수행한다
사실 bfs를 사용하면 O(n^2)으로도 경로 탐색을 할 수 있다. 모든 육지를 Queue에 넣고 bfs를 한 번만 수행하는 것이다.
방문된 곳은 이동 거리와 어떤 섬에서부터 방문했는지를 표시한다. 그리고 다른 섬 or 다른 섬에서 방문한 바다를 만났을 때, (자신이 이동한 거리) + (다른 섬이 이동한 거리)가 최단 거리가 된다. 모든 지점이 돌아가면서 한 칸씩만 이동하기 때문이다.
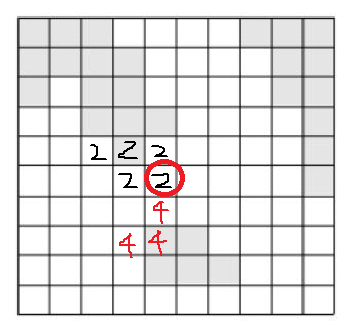

(1)방문 표시 + (2)이동 거리 + (3)어떤 섬에서 방문했는지 표시해야 하기 때문에 복잡해서 떠올리기가 어려웠던 것 같다.
나는 그림처럼 방문한 바다에는 시작 지점의 라벨을 저장해서 방문 표시와 어떤 섬에서 시작했는지를 한번에 나타냈는데, 좀 헷갈렸어서 방문 체크를 위한 배열을 따로 사용하는 것도 좋을 것 같다. 이동 거리를 저장하는 배열은 따로 선언했다.
코드 (방법1)
import java.io.BufferedReader
import java.io.InputStreamReader
import java.util.*
import kotlin.math.min
val dRow = arrayOf(-1, 1, 0, 0)
val dCol = arrayOf(0, 0, -1, 1)
fun main() = with(BufferedReader(InputStreamReader(System.`in`))) {
val n = readLine().toInt()
val graph = Array(n) { // 그래프 입력 받아서 저장
StringTokenizer(readLine()).let { st ->
IntArray(n) { st.nextToken().toInt() }
}
}
var label = 2 // 중복 방문 체크를 위해 2부터 시작
for (i in 0 until n) {
for (j in 0 until n) {
if (graph[i][j] == 1) {
graph[i][j] = label // 섬 분류
labelingDfs(graph, i, j, label++)
}
}
}
var answer = Integer.MAX_VALUE
for (i in 0 until n) { // 모든 육지마다 최단 경로 탐색
for (j in 0 until n) {
if (graph[i][j] > 1) {
val copiedGraph = copyGraph(graph) // bfs 수행할 때마다 그래프 복제해야 함
answer = min(answer, bfs(copiedGraph, i, j))
}
}
}
print(answer)
}
fun labelingDfs(graph: Array<IntArray>, row: Int, col: Int, label: Int) {
for (i in 0 until 4) {
val newRow = row + dRow[i]
val newCol = col + dCol[i]
if (newRow in graph.indices && newCol in graph.indices && graph[newRow][newCol] == 1) {
graph[newRow][newCol] = label // 방문 체크 + 섬 라벨링
labelingDfs(graph, newRow, newCol, label)
}
}
}
fun copyGraph(graph: Array<IntArray>): Array<IntArray>{
val tempGraph = Array(graph.size){IntArray(graph.size)}
for (i in graph.indices) {
for (j in graph.indices){
tempGraph[i][j] = graph[i][j]
}
}
return tempGraph
}
fun bfs(graph: Array<IntArray>, startRow: Int, startCol: Int): Int {
var distance = 0
val label = graph[startRow][startCol]
val queue: Queue<Pair<Int, Int>> = LinkedList()
queue.offer(Pair(startRow, startCol))
while (queue.isNotEmpty()) {
val size = queue.size
// 다리를 한 번씩 모두 늘리면 distance 증가
repeat(size) {
val pair = queue.poll()
val row = pair.first
val col = pair.second
for (i in 0 until 4) {
val newRow = row + dRow[i]
val newCol = col + dCol[i]
if (newRow in graph.indices && newCol in graph.indices) {
// 방문하지 않았던 바다
if (graph[newRow][newCol] == 0) {
graph[newRow][newCol] = label
queue.offer(Pair(newRow, newCol))
}
// 바다도 아니고 같은 섬도 아니다 -> 다른 섬에 도착
else if (graph[newRow][newCol] != label) {
return distance // 경로 이동 횟수 반환
}
}
}
}
distance++
}
return Integer.MAX_VALUE // 섬 중앙에서 시작했을 때
}
코드 (방법2)
import java.io.BufferedReader
import java.io.InputStreamReader
import java.util.*
val dRow = arrayOf(-1, 1, 0, 0)
val dCol = arrayOf(0, 0, -1, 1)
val queue: Queue<Pair<Int, Int>> = LinkedList()
fun main() = with(BufferedReader(InputStreamReader(System.`in`))) {
val n = readLine().toInt()
val graph = Array(n) { // 그래프 입력 받아서 저장
StringTokenizer(readLine()).let { st ->
IntArray(n) { st.nextToken().toInt() }
}
}
var label = 2 // 중복 방문 체크를 위해 2부터 시작
for (i in 0 until n) {
for (j in 0 until n) {
if (graph[i][j] == 1) {
graph[i][j] = label // 섬 분류
labelingDfs(graph, i, j, label++)
}
}
}
val answer = bfs(graph) // bfs로 최단 경로 탐색
print(answer)
}
fun labelingDfs(graph: Array<IntArray>, row: Int, col: Int, label: Int) {
var isEdge = false // 섬의 육지 중 테두리를 찾기 위한 플래그
for (i in 0 until 4) {
val newRow = row + dRow[i]
val newCol = col + dCol[i]
if (newRow in graph.indices && newCol in graph.indices && graph[newRow][newCol] != label) {
if (graph[newRow][newCol] == 0) { // 주변에 바다가 있다 -> 섬의 테두리이다
isEdge = true
continue
}
graph[newRow][newCol] = label
labelingDfs(graph, newRow, newCol, label)
}
}
if (isEdge) queue.add(Pair(row, col)) // 섬의 테두리에서만 bfs 시작
}
fun bfs(graph: Array<IntArray>): Int {
val lengthGraph = Array(graph.size) { IntArray(graph.size) } // 이동 거리 저장하는 배열
while (queue.isNotEmpty()) {
val pair = queue.poll()
val row = pair.first
val col = pair.second
for (i in 0 until 4) {
val newRow = row + dRow[i]
val newCol = col + dCol[i]
// 그래프 바깥이거나 해당 라벨에서 이미 방문했던 곳 or 같은 섬이면 건너뛴다
if (newRow !in graph.indices || newCol !in graph.indices || graph[newRow][newCol] == graph[row][col]) {
continue
}
// 0이 아니다 -> 다른 라벨이 방문했던 곳 or 다른 라벨의 섬 -> 최단 경로 탐색 완료
if (graph[newRow][newCol] != 0) {
return lengthGraph[row][col] + lengthGraph[newRow][newCol]
}
graph[newRow][newCol] = graph[row][col] // 시작점의 라벨로 설정
lengthGraph[newRow][newCol] = lengthGraph[row][col] + 1 // 이동 거리
queue.offer(Pair(newRow, newCol))
}
}
return 0
}'Problem Solving > 백준' 카테고리의 다른 글
| 백준 1654번: 랜선 자르기 (Kotlin) (0) | 2021.12.27 |
|---|---|
| 백준 1167번: 트리의 지름 (0) | 2021.12.25 |
| 백준 7576번: 토마토 (Kotlin) (0) | 2021.12.23 |
| 백준 9466번: 텀 프로젝트 (Kotlin) (0) | 2021.12.22 |
| 백준 1406번: 에디터 (Kotlin) (0) | 2021.12.16 |